Projects¶
This section contains some of my class and personal projects that fall under the following broad fields:
- Uncertainty Quantification and Inference
- Machine Learning
- Numerical Methods and Numerical Differential Equations.
Uncertainty Quantification and Inference¶
Data Assimilative Path Planning¶
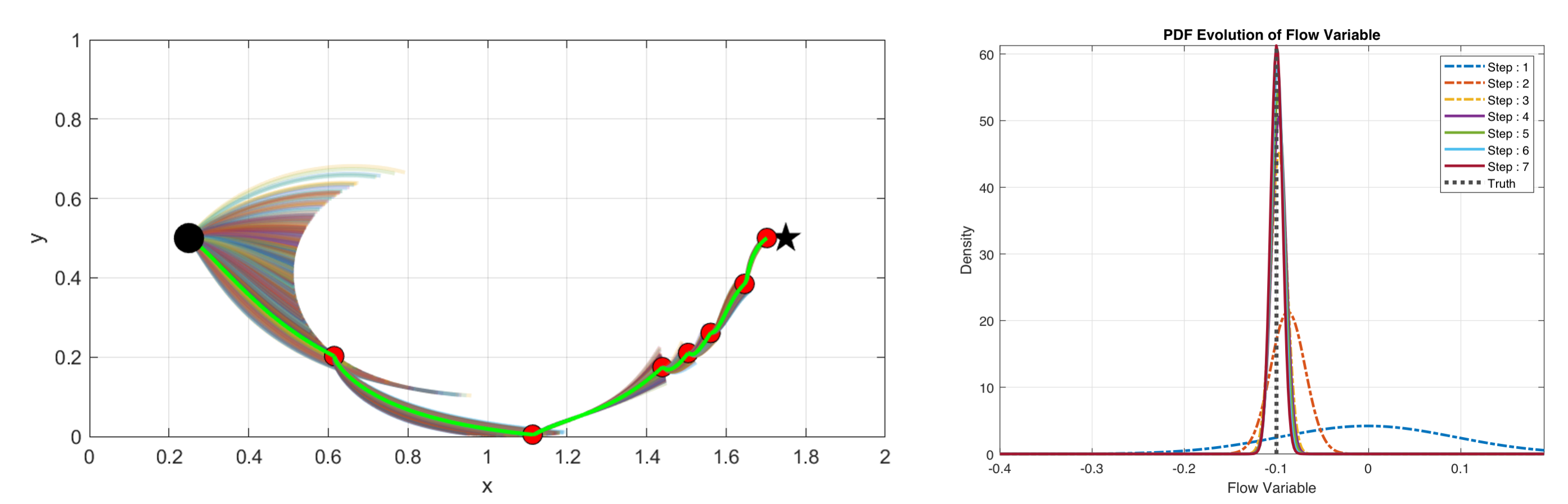
A significant challenge in path planning for autonomous underwater and surface vehicles is navigating ocean environments that are highly uncertain. Users often lack accurate information or reliable forecasts of ocean currents and velocity fields, both of which have a substantial influence on vehicle navigation. As part of the class 16.S498 (Risk-Aware and Robust Nonlinear Planning), I collaborated with a teammate to investigate path planning in such uncertain environments and explore how data assimilation can be incorporated into the general path planning framework. By using measurements collected by the vehicle, we examined how Bayesian filtering could reduce environmental uncertainty and dynamically update the vehicle's path, enabling it to navigate both safely and efficiently to its target.
The figure above illustrates a sample result from the proposed algorithm for a simple case involving navigation in an uncertain flow field parameterized by a single random variable. Left subfigure: The possible paths taken by the vehicle for a fixed sequence of controls over short time intervals show high uncertainty initially, which progressively diminishes as measurements are collected and environmental uncertainty is reduced. Right subfigure: The evolution of the probability density function (PDF) of the random flow variable demonstrates convergence to the true value as more data is gathered, achieving the desired reduction in uncertainty.
Check out the full project report at this link -->
Variational Methods for Bayesian Inference¶
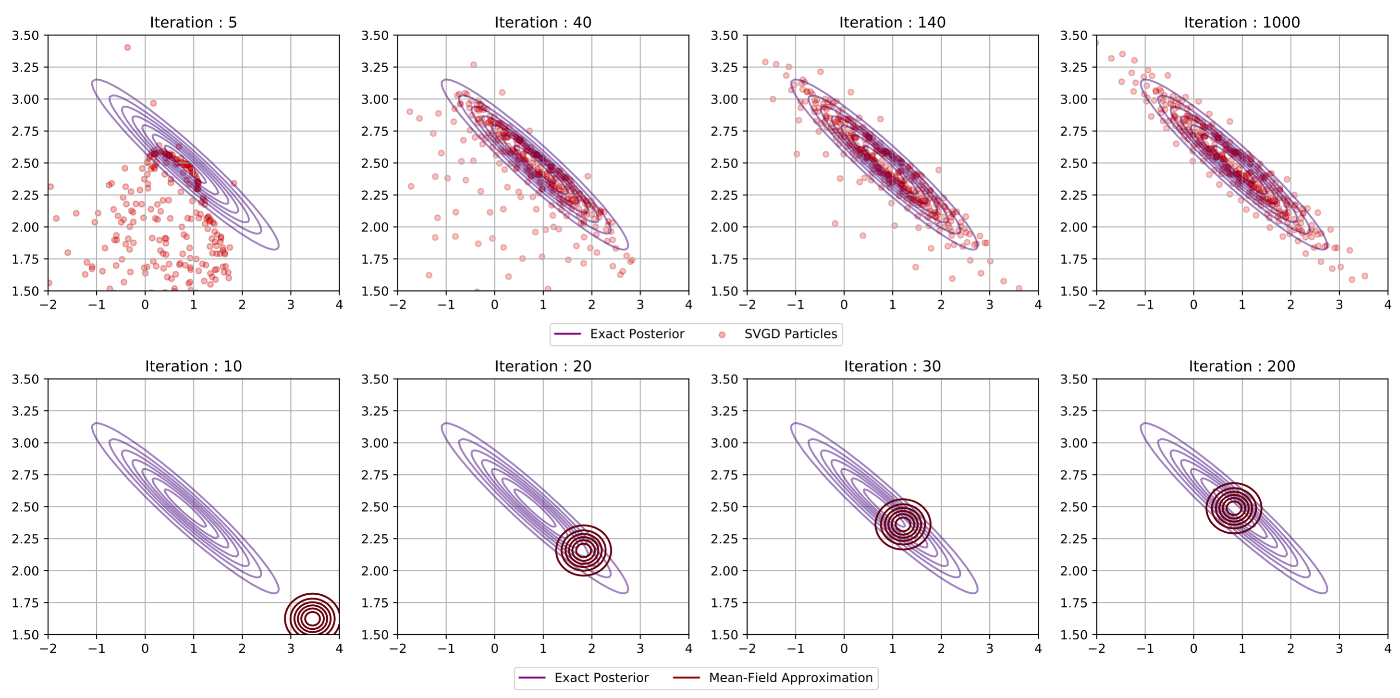
A central task in Bayesian inference is the ability to accurately approximate and sample from the posterior distribution. As part of the class 16.940 (Numerical Methods for Stochastic Modeling and Inference) I looked at investigating one such family of methods that performs this task: variational methods. Variational inference reformulates the problem of approximating or sampling from the posterior as a deterministic optimization problem. The optimization is in general framed as finding a simpler distribution within a given family of densities (for example the exponential family) that best approximates the target distribution. In this project, we investigated two variational approaches, each falling in distinct categories: Stein variational methods for inference (a non-parametric approach) and mean-field variational inference (a parametric approach).
The figure above shows a sample result from this project for when the same posterior distribution is approximated using each approach. Stein's method (top row) uses a set of particles that are optimally moved to represent the posterior whereas the mean-field approach (bottom row) optimizes the hyperparameters of some candidate distribution belonging to some predefined family of densities.
Check out the full project report at this link -->
Machine Learning and Statistical Learning Theory¶
Residual RNN Architectures Based on ODE Stability Theory¶
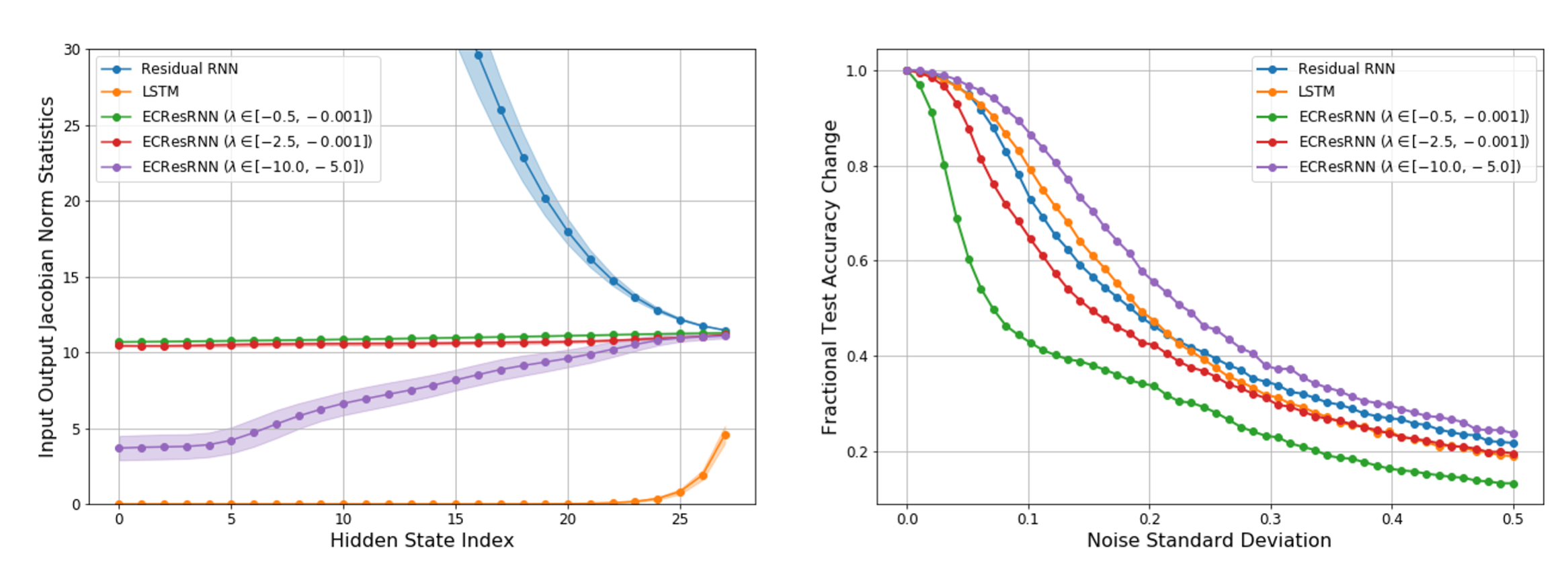
The interpretation of deep learning architectures as time integration schemes and flow maps for dynamical systems has garnered much attention in recent years and led to numerous advancements ranging from Neural Ordinary Differential Equations to novel network architectures based on established time integration schemes (such as Runge-Kutta and Leap-frog methods). In this project, we aimed to follow along this trend to motivate the design of recurrent neural networks (RNNs). In particular, we looked at using the stability theory of ODEs and dynamical systems to investigate a new RNN architecture that aims to tackle two big issues in typical recurrent networks: (1) vanishing/exploding gradients and (2) robustness to input noise. We are currently working to convert this project into a paper, and will provide the link to that given paper for further details once it has been completed.
Numerical Methods¶
The Adaptive Finite Element Method¶
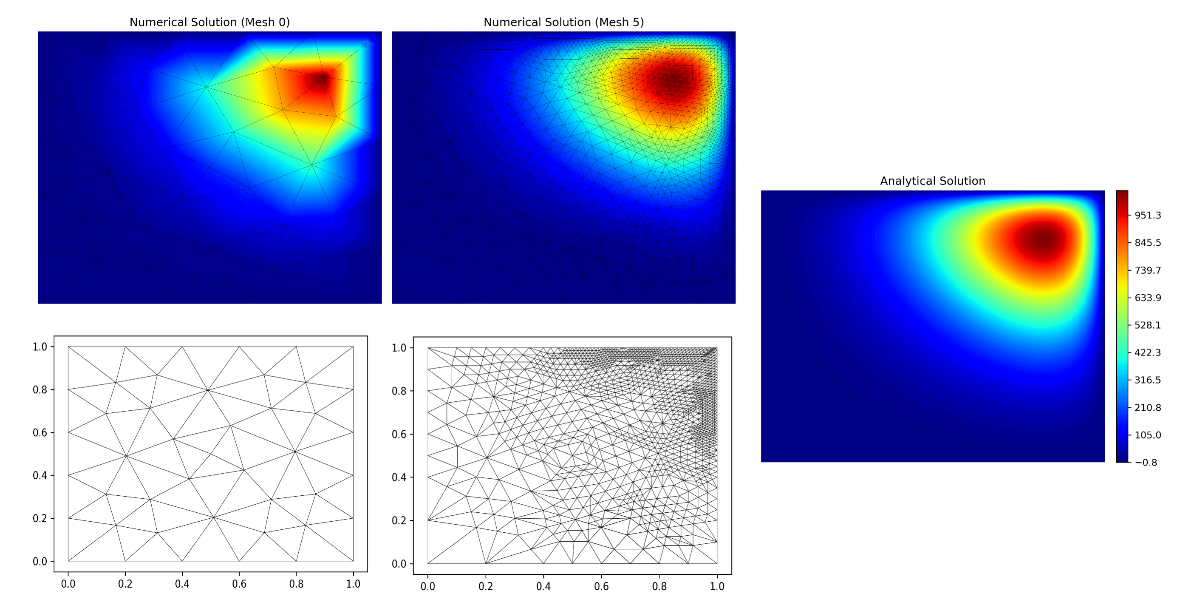
A topic that has always fascinated me is adaptive mesh refinement, where the solver can automatically identify regions of the domain with high solution error and refine the mesh locally in those areas. As part of the class 2.097 (Numerical Methods for PDEs), I decided to explore adaptive methods in detail by focusing on the h-adaptive finite element method. This project involved coding from scratch: (1) a continuous Galerkin solver for unstructured domains, (2) an error estimation scheme (based on the work of Babuška et al.) to determine where the mesh should be refined, and (3) a mesh refinement algorithm to split elements while maintaining proper mesh quality.
The figure above illustrates a sample result from the final code, which successfully refined the mesh in the top-right corner of the domain, where the solution required higher resolution to accurately resolve the numerical solution.
Check out the full project report at this link -->
Check out the code on Github at this link -->
Acceleration Techniques for Restarted GMRES¶
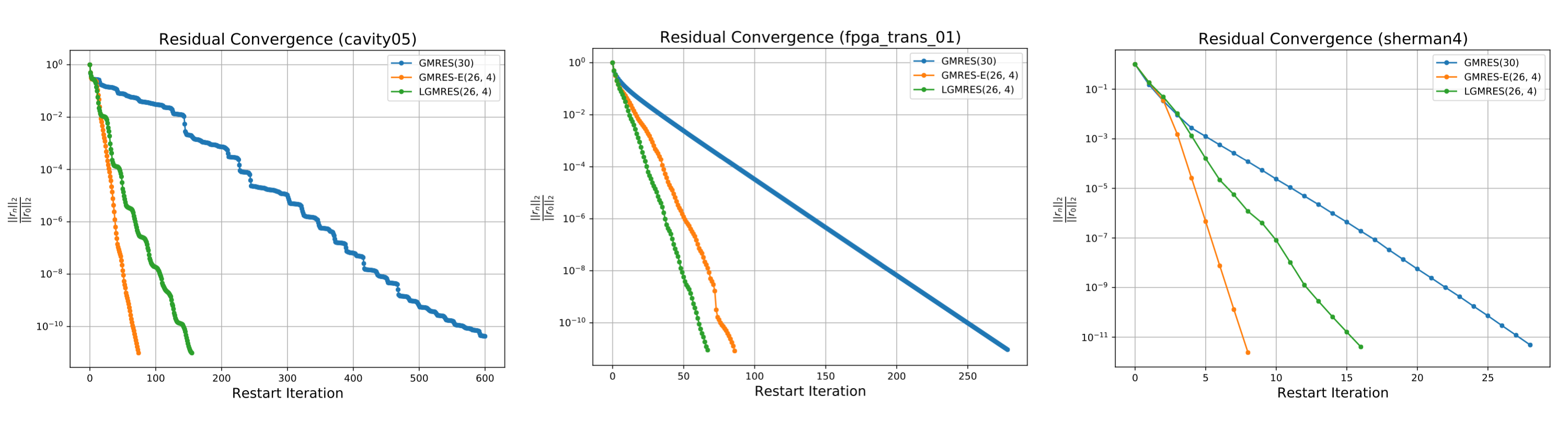
GMRES has become a very popular algorithm in industry applications for iteratively solving nonsymmetric systems of linear equations. A key issue however is that, due to computer memory constraints, the algorithm typically requires to be "restarted" every few iterations (the best guess for the linear system's solution at the end of one restart cycle ends up being the initial guess for the next restart cycle and the process continues until convergence).
This restarting process can unfortunately weaken the convergence rate of the overall algorithm. As part of the class 18.335 (Numerical Linear Algebra), I therefore looked into acceleration techniques for restarted GMRES that aims to address this issue. In particular, I implemented and investigated the GMRES-E and LGMRES algorithms in Python and compared them to standard GMRES for some canonical test problems (sample convergence results are shown in the figure above).