Research¶
MIT - MSEAS Research Group¶
Time-Optimal Path Planning under Harvesting Constraints¶
Path planning for autonomous surface and underwater vehicles has garnered significant attention over the past few decades. Our research focused on generating time-optimal paths under constraints where the vehicle must harvest a specified amount of a field from the environment (e.g., energy, marine plastic pollution) before reaching its target. Using a PDE-based approach, we were able to compute globally optimal solutions to this path planning problem.
Acoustic Modeling in Uncertain Environments¶
Since electromagnetic waves attenuate in water, underwater communication and navigation rely on acoustic methods. Accurate acoustic propagation models are critical for marine applications, but the ocean's highly uncertain environment presents significant challenges. This project focused on modeling high-frequency acoustic propagation in uncertain ocean environments, where uncertainties arise from factors such as the sound speed profile and acoustic source location.
Our approach utilized level set methods to model acoustic wavefront propagation, coupled with a reduced-order technique (the Dynamically Orthogonal (DO) equations) to quantify uncertainty in the wavefront after propagating through the unknown environment. Additionally, we developed novel schemes for acoustic Bayesian inference using measurements.
The figure above illustrates a sample result from our level set approach in a deterministic environment. To handle wavefront intersections, we represented the wavefront in an augmented phase space as the intersection of two level sets (left-most subfigure). The resulting wavefront's propagation in the physical domain, modeled as a channel with a curved bottom, is shown in the right-most subfigure.
McGill Computational Aerodynamics Group¶
Adjoint Based Aerodynamic Shape Optimization for High Order Methods¶
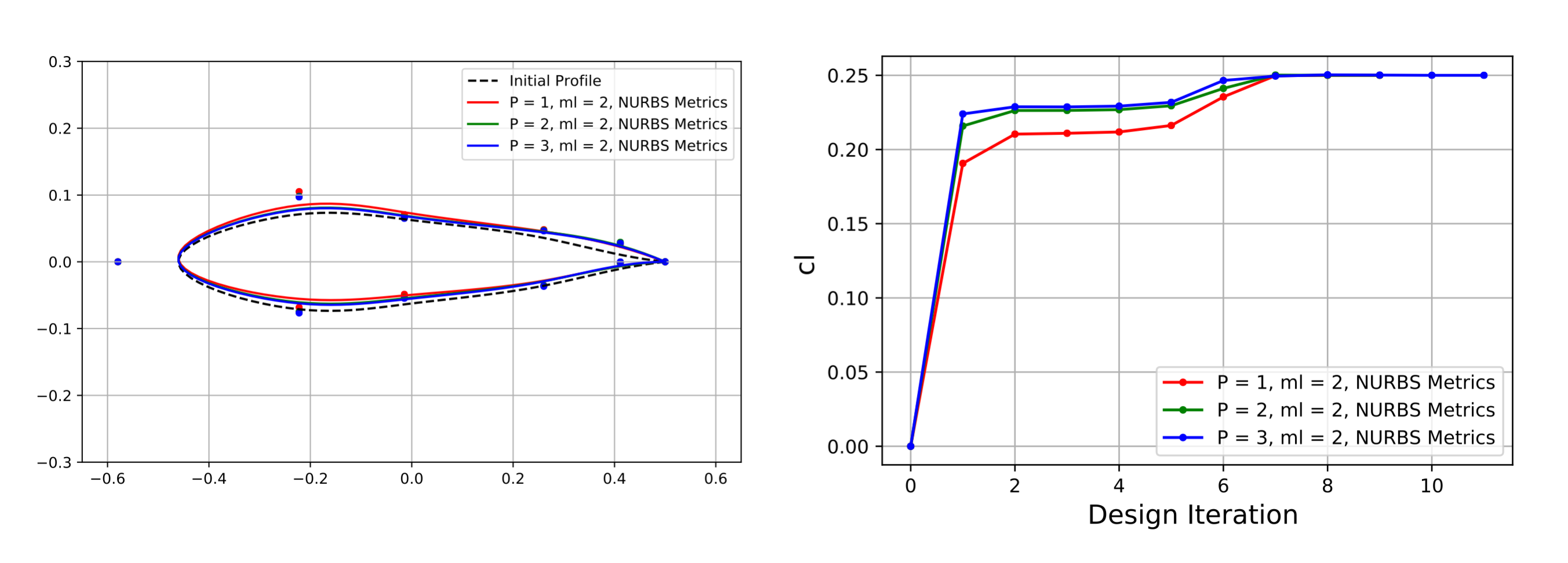
High order methods are being increasingly studied as approaches for numerically simulating flows as they allow for much higher accuracy as compared to traditional finite volume CFD solvers. This research project looked at joining adjoint based optimization (an efficient method for gradient based optimization) with these high order methods in order to tackle aerospace design problems.
Free Form Deformation for Aerodynamic Shape Optimization¶
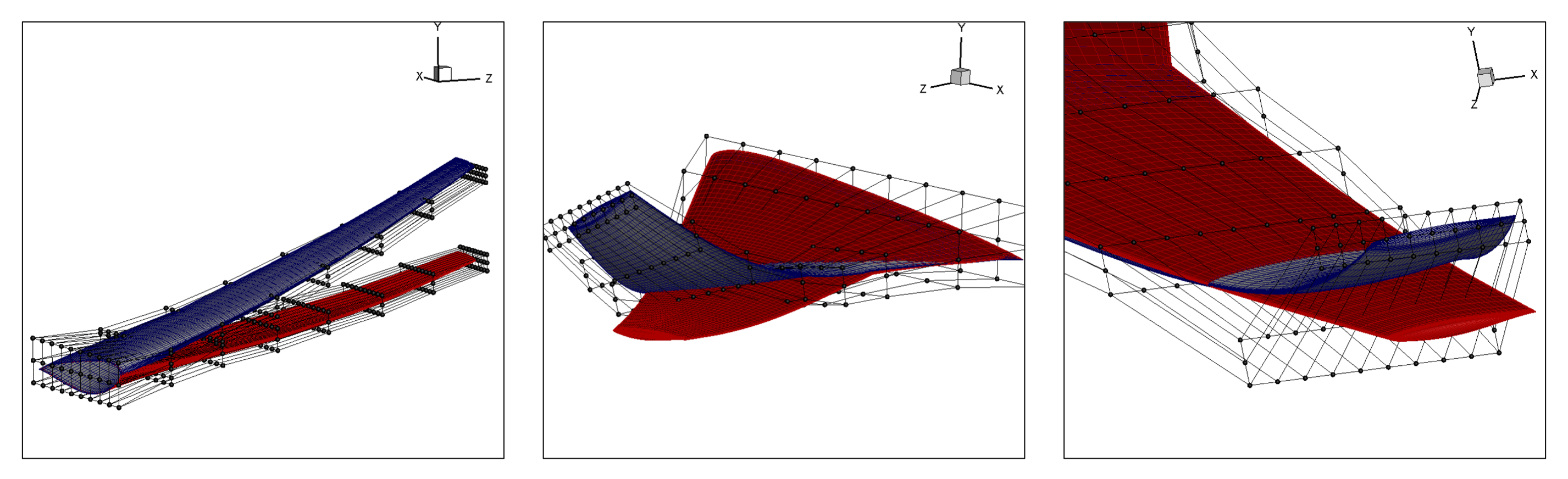
A significant challenge in aerodynamic shape optimization is determining how to represent the object of interest so it can be optimized efficiently — this task is referred to as shape parameterization. For instance, if a wing were to be optimized, one approach is to discretely represent the wing surface using a mesh of triangles (e.g., using Delaunay triangulation) and treat the vertices of these triangles as the degrees of freedom. However, this approach can lead to thousands, or even millions, of design parameters in the optimization problem, making it computationally expensive to solve. Moreover, it may produce shapes that lack sufficient smoothness.
During the summer of my sophomore year, I worked on a project exploring a shape parameterization method known as Free Form Deformation (FFD). Originating from computer graphics, FFD involves constructing a lattice of control points around an object of interest. These control points can be manipulated to deform the shape enclosed by the lattice. This method significantly reduces the number of degrees of freedom in the optimization problem while allowing for the generation of smooth candidate shapes. My work focused on developing techniques to create tight-fitting FFD boxes around arbitrarily shaped objects and on designing interconnected FFD boxes to enable better local shape control while maintaining surface continuity. The figure above illustrates examples of a wing's deformation using an FFD lattice.
At the end of the summer, we were invited to present our work to Bombardier Aerospace's Advanced Aerodynamics Group, discussing the potential applications of FFD in aerospace design. The slides for this talk can be found at this link.